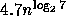 operations, where
operations, where
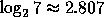 .
.
The Level 3 BLAS specifications [28] specify the input, output
and calling sequence for each routine, but allow freedom of
implementation, subject to the requirement that the routines be
numerically stable .
Level 3 BLAS implementations can therefore be
built using matrix multiplication algorithms that achieve a more
favorable operation count (for suitable dimensions) than the standard
multiplication technique, provided that these ``fast'' algorithms are
numerically stable. The simplest fast matrix multiplication
technique is Strassen's
method , which can
multiply two n-by-n
matrices in fewer than 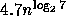 operations, where
operations, where
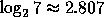 .
.
The effect on the results in this chapter of using a fast Level 3 BLAS implementation can be explained as follows. In general, reasonably implemented fast Level 3 BLAS preserve all the bounds presented here (except those at the end of subsection 4.10), but the constant p(n) may increase somewhat. Also, the iterative refinement routine xyyRFS may take more steps to converge.
This is what we mean by reasonably implemented fast Level 3 BLAS.
Here, 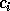 denotes a constant depending on the specified matrix dimensions.
denotes a constant depending on the specified matrix dimensions.
(1) If A is m-by-n, B is n-by-p and 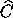 is the computed
approximation to C = AB, then
is the computed
approximation to C = AB, then
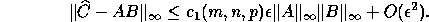
(2) The computed solution

to the triangular systems TX = B, where T is m-by-m and B is m-by-p, satisfies
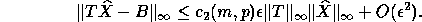
For conventional Level 3 BLAS implementations these conditions hold with

and
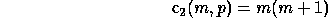
. Strassen's method satisfies these bounds for slightly larger

and

.
For further details, and references to fast multiplication techniques, see [20].