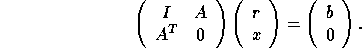Further Details: Error Bounds for Linear Least Squares
Problems





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
The conventional error analysis of linear least squares problems goes
as follows .
As above, let 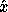 be the solution to minimizing
be the solution to minimizing
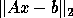 computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection 2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank [45]:
computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection 2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank [45]:
The computed solution 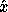 has a small normwise backward error.
In other words
has a small normwise backward error.
In other words 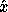 minimizes
minimizes 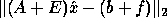 , where
E and f satisfy
, where
E and f satisfy
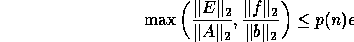
and p(n) is a modestly growing function of n. We take p(n) = 1 in
the code fragments above.
Let 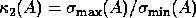 (approximated by
1/RCOND in the above code fragments),
(approximated by
1/RCOND in the above code fragments),
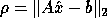 (= RNORM above), and
(= RNORM above), and 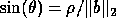 (SINT = RNORM / BNORM above). Here,
(SINT = RNORM / BNORM above). Here,  is the acute angle between
the vectors
is the acute angle between
the vectors 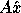 and
and 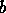 .
Then when
.
Then when 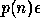 is small, the error
is small, the error 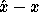 is bounded by
is bounded by
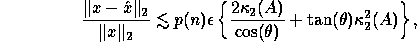
where 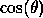 = COST and
= COST and 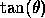 = TANT in the code fragments
above.
= TANT in the code fragments
above.
We avoid overflow by making sure RCOND and COST are both at least
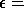 EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
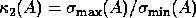 may be computed directly
from the singular values of A returned by xGELSS (as in the code fragment) or
by xGESVD. It may also be approximated by using xTRCON following calls to
xGELS or xGELSX. xTRCON estimates
may be computed directly
from the singular values of A returned by xGELSS (as in the code fragment) or
by xGESVD. It may also be approximated by using xTRCON following calls to
xGELS or xGELSX. xTRCON estimates 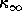 or
or 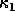 instead
of
instead
of 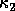 , but these can differ from
, but these can differ from 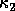 by at most a factor of n.
by at most a factor of n.
If A is rank-deficient, xGELSS and xGELSX can be used to regularize the
problem
by treating all singular values
less than a user-specified threshold
(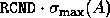 ) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See [45] for error bounds in this case, as well as
[45][19] for the
underdetermined
case.
) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See [45] for error bounds in this case, as well as
[45][19] for the
underdetermined
case.
The solution of the overdetermined,
full-rank problem may also be
characterized as the solution of the linear system of equations
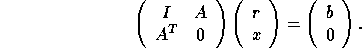
By solving this linear system using xyyRFS or xyySVX (see section
4.4) componentwise error bounds can also be obtained
[7].





Next: Error Bounds for
Up: Error Bounds for
Previous: Error Bounds for
Tue Nov 29 14:03:33 EST 1994
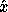 be the solution to minimizing
be the solution to minimizing
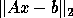 computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection 2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank [45]:
computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection 2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank [45]:
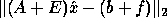 , where
E and f satisfy
, where
E and f satisfy
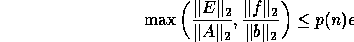
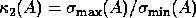 (approximated by
1/RCOND in the above code fragments),
(approximated by
1/RCOND in the above code fragments),
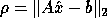 (= RNORM above), and
(= RNORM above), and 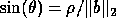 (SINT = RNORM / BNORM above). Here,
(SINT = RNORM / BNORM above). Here,  is the acute angle between
the vectors
is the acute angle between
the vectors 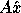 and
and 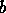 .
.
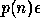 is small, the error
is small, the error 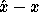 is bounded by
is bounded by 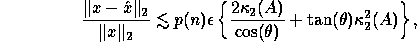
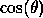 = COST and
= COST and 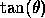 = TANT in the code fragments
above.
= TANT in the code fragments
above.
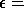 EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
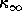 or
or 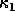 instead
of
instead
of 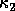 , but these can differ from
, but these can differ from 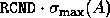 ) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See
) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See