Improved Error Bounds





Next: Error Bounds for
Up: Further Details: How
Previous: Standard Error Analysis
The standard error analysis just outlined has a drawback: by using the
infinity norm 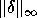 to measure the backward error,
entries of equal magnitude in
to measure the backward error,
entries of equal magnitude in  contribute equally to the final
error bound
contribute equally to the final
error bound 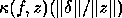 . This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
. This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
For example, consider solving a diagonal system of linear equations Ax = b.
Each component of the solution is computed accurately by
Gaussian elimination: 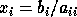 .
The usual error bound is approximately
.
The usual error bound is approximately
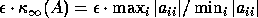 ,
which can arbitrarily overestimate the true error,
,
which can arbitrarily overestimate the true error,  , if at least one
, if at least one
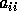 is tiny and another one is large.
is tiny and another one is large.
LAPACK addresses this inadequacy by providing some algorithms
whose backward error  is a tiny relative change in
each component of z:
is a tiny relative change in
each component of z: 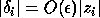 .
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error
.
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error .
.
If the input data has independent uncertainty in each component,
each component must have at least a small relative uncertainty,
since each is a floating-point number.
In this case, the extra uncertainty contributed by the algorithm is not much
worse than the uncertainty in the input data, so
one could say the answer provided by a componentwise
relatively backward stable algorithm is as accurate as the data
warrants [1].
When solving Ax = b using expert driver xyySVX or computational routine xyyRFS,
for example, we almost always
compute 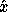 satisfying
satisfying 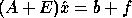 , where
, where
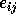 is a small relative change in
is a small relative change in 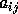 and
and
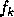 is a small relative change in
is a small relative change in 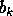 . In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
. In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
LAPACK can achieve this accuracy
for linear equation solving,
the bidiagonal singular value decomposition, and
the symmetric tridiagonal eigenproblem,
and provides facilities for achieving this accuracy for least squares problems.
Future versions of LAPACK will also achieve this
accuracy for other linear algebra problems, as discussed below.





Next: Error Bounds for
Up: Further Details: How
Previous: Standard Error Analysis
Tue Nov 29 14:03:33 EST 1994
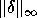 to measure the backward error,
entries of equal magnitude in
to measure the backward error,
entries of equal magnitude in  contribute equally to the final
error bound
contribute equally to the final
error bound 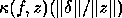 . This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
. This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
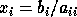 .
The usual error bound is approximately
.
The usual error bound is approximately
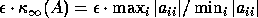 ,
which can arbitrarily overestimate the true error,
,
which can arbitrarily overestimate the true error,  , if at least one
, if at least one
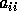 is tiny and another one is large.
is tiny and another one is large.
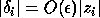 .
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error
.
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error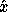 satisfying
satisfying 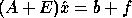 , where
, where
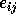 is a small relative change in
is a small relative change in 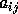 and
and
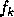 is a small relative change in
is a small relative change in 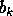 . In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
. In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).