Generalized Nonsymmetric Eigenproblems





Next: Generalized (or Quotient)
Up: Computational Routines
Previous: Generalized Symmetric Definite
Let A and B be n-by-n matrices.
A scalar 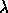 is called a generalized eigenvalue and a
non-zero column vector x the corresponding right generalized eigenvector
if
is called a generalized eigenvalue and a
non-zero column vector x the corresponding right generalized eigenvector
if 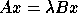 .
A non-zero column vector y satisfying
.
A non-zero column vector y satisfying 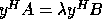 (where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to
(where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to 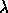 .
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
.
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
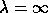 , by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
, by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
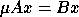 is perfectly well-behaved, and the infinite eigenvalue
corresponds to
is perfectly well-behaved, and the infinite eigenvalue
corresponds to 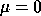 .
To deal with infinite eigenvalues,
the LAPACK routines return two values,
.
To deal with infinite eigenvalues,
the LAPACK routines return two values,
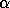 and
and 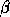 ,
for each eigenvalue
,
for each eigenvalue 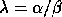 .
The first basic task of these routines is to compute the
all n pairs
.
The first basic task of these routines is to compute the
all n pairs 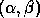 and x and/or y for a given
pair of matrices A,B.
and x and/or y for a given
pair of matrices A,B.
If the determinant of 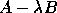 is zero for all values of
is zero for all values of 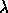 ,
the eigenvalue problem is called singular, and is signaled by some
,
the eigenvalue problem is called singular, and is signaled by some
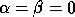 (in the presence of roundoff,
(in the presence of roundoff, 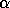 and
and 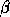 may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of
may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of 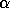 and
and 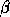 may be
indeterminate [43][21][80][71].
may be
indeterminate [43][21][80][71].
The other basic task is to compute the
generalized Schur decomposition of the pair A,B.
If A and B are complex,
then the pair's generalized Schur decomposition is
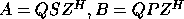 , where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P to have
non-negative diagonal entries. Note that in this form,
the eigenvalues can be easily computed from the diagonals:
, where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P to have
non-negative diagonal entries. Note that in this form,
the eigenvalues can be easily computed from the diagonals:
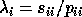 ,
and so the LAPACK routines return
,
and so the LAPACK routines return
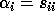 and
and 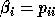 . The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
. The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
If A and B are real,
then the pair's generalized Schur decomposition is
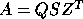 ,
, 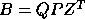 ,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P is normalized so that diagonal
entries of P
corresponding to 1-by-1 blocks of S are non-negative,
while the (upper triangular) diagonal blocks of P corresponding
to 2-by-2 blocks of S are made diagonal.
Note that for real eigenvalues,
as for all eigenvalues in the complex case,
the
,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P is normalized so that diagonal
entries of P
corresponding to 1-by-1 blocks of S are non-negative,
while the (upper triangular) diagonal blocks of P corresponding
to 2-by-2 blocks of S are made diagonal.
Note that for real eigenvalues,
as for all eigenvalues in the complex case,
the 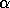 and
and 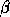 values corresponding to real eigenvalues
may be easily computed from the diagonal of S and P.
The
values corresponding to real eigenvalues
may be easily computed from the diagonal of S and P.
The 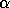 and
and 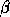 values corresponding to complex
eigenvalues are computed by computing
values corresponding to complex
eigenvalues are computed by computing 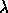 ,
then computing the
,
then computing the 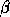 values that would result if
the 2-by-2 diagonal block of S,P were upper triangularized using
unitary transformations ,
and finally multiplying to get
values that would result if
the 2-by-2 diagonal block of S,P were upper triangularized using
unitary transformations ,
and finally multiplying to get 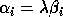 and
and 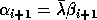 .
.
The columns of Q and Z are called generalized Schur vectors
and span pairs of deflating subspaces of A and B [72].
Deflating subspaces are a generalization of invariant subspaces:
The first k columns of Z span a right deflating subspace
mapped by both A and B into a left deflating subspace spanned by
the first k columns of Q. This pair of deflating subspaces corresponds
to the first k eigenvalues appearing at the top of S and p.
The computations proceed in the following stages:
- The pair A,B is reduced to generalized upper Hessenberg form.
If A and B are real this decomposition is
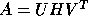 ,
, 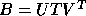 where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is
where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is 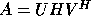 ,
, 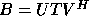 with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
which computes H and T and optionally U and/or V.
Note that in contrast to xGEHRD (for the standard
nonsymmetric eigenvalue problem),
xGGHRD does not compute U and V in a factored form.
with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
which computes H and T and optionally U and/or V.
Note that in contrast to xGEHRD (for the standard
nonsymmetric eigenvalue problem),
xGGHRD does not compute U and V in a factored form.
- The pair H,T is reduced to generalized Schur form
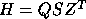 ,
, 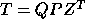 (for H and T real) or
(for H and T real) or
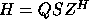 ,
, 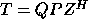 (for H and T complex) by subroutine xHGEQZ.
The values
(for H and T complex) by subroutine xHGEQZ.
The values 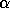 and
and 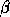 are also computed.
The matrices Z and Q are optionally computed.
are also computed.
The matrices Z and Q are optionally computed.
- The left and/or right eigenvectors of the pair A
are computed by xTGEVC.
One may optionally transform the right eigenvectors of S,P
to the right eigenvectors of A,B (or of H,T) by passing
UQ,VZ (or Q,Z) to xTGEVC.
In addition, the routines xGGBAL and xGGBAK
may be used to balance the
pair A,B prior to reduction to generalized Hessenberg form.
Balancing involves
premultiplying A and B by one permutation
and postmultiplying them by another,
to try to make A,B as nearly triangular
as possible,
and then ``scaling'' the matrices by
premultiplying A and B by one diagonal
matrix and postmultiplying by another in order to
make the rows and columns of A and B
as close in norm to 1 as possible.
These transformations can improve speed and
accuracy of later processing in some cases;
however, the scaling step can sometimes make
things worse.
Moreover,
the scaling step will significantly change the generalized
Schur form that results.
xGGBAL performs the balancing,
and xGGBAK back transforms the eigenvectors of the balanced matrix pair.
--------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
--------------------------------------------------------------------------
general Hessenberg reduction SGGHRD CGGHRD DGGHRD ZGGHRD
balancing SGGBAL CGGBAL DGGBAL ZGGBAL
back transforming SGGBAK CGGBAK DGGBAK ZGGBAK
--------------------------------------------------------------------------
Hessenberg Schur factorization SHGEQZ CHGEQZ DHGEQZ ZHGEQZ
--------------------------------------------------------------------------
(quasi)triangular eigenvectors STGEVC CTGEVC DTGEVC ZTGEVC
--------------------------------------------------------------------------
Table 2.15: Computational routines for the generalized nonsymmetric eigenproblem
A future release of LAPACK will include the routines xTGEXC, xTGSYL, xTGSNA
and xTGSEN, which are analogous to the routines xTREXC, xTRSYL, xTRSNA and
xTRSEN. They will
reorder eigenvalues in generalized Schur form, solve the generalized
Sylvester equation, compute condition numbers of generalized eigenvalues and
eigenvectors, and compute condition numbers of average eigenvalues and deflating
subspaces.





Next: Generalized (or Quotient)
Up: Computational Routines
Previous: Generalized Symmetric Definite
Tue Nov 29 14:03:33 EST 1994
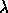 is called a generalized eigenvalue and a
non-zero column vector x the corresponding right generalized eigenvector
if
is called a generalized eigenvalue and a
non-zero column vector x the corresponding right generalized eigenvector
if 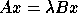 .
A non-zero column vector y satisfying
.
A non-zero column vector y satisfying 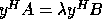 (where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to
(where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to 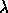 .
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
.
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
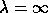 , by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
, by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
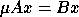 is perfectly well-behaved, and the infinite eigenvalue
corresponds to
is perfectly well-behaved, and the infinite eigenvalue
corresponds to 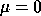 .
To deal with infinite eigenvalues,
the LAPACK routines return two values,
.
To deal with infinite eigenvalues,
the LAPACK routines return two values,
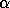 and
and 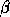 ,
for each eigenvalue
,
for each eigenvalue 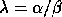 .
The first basic task of these routines is to compute the
all n pairs
.
The first basic task of these routines is to compute the
all n pairs 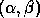 and x and/or y for a given
pair of matrices A,B.
and x and/or y for a given
pair of matrices A,B.
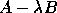 is zero for all values of
is zero for all values of 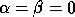 (in the presence of roundoff,
(in the presence of roundoff, 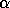 and
and 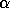 and
and 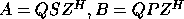 , where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P
, where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P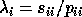 ,
and so the LAPACK routines return
,
and so the LAPACK routines return
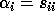 and
and 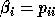 . The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
. The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
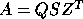 ,
, 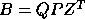 ,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P
,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P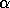 and
and 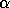 and
and 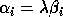 and
and 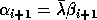 .
.
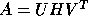 ,
, 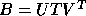 where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is
where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is 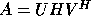 ,
, 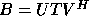 with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
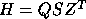 ,
, 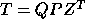 (for H and T real) or
(for H and T real) or
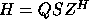 ,
, 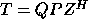 (for H and T complex) by subroutine xHGEQZ.
(for H and T complex) by subroutine xHGEQZ.
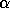 and
and