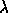 is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if
is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if 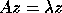 .
. 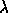 is
always real when A is real symmetric or complex Hermitian.
is
always real when A is real symmetric or complex Hermitian.
Let A be a real symmetric or
complex Hermitian n-by-n matrix.
A scalar 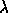 is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if
is called an eigenvalue and a nonzero column vector
z the corresponding eigenvector if 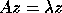 .
. 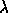 is
always real when A is real symmetric or complex Hermitian.
is
always real when A is real symmetric or complex Hermitian.
The basic task of the symmetric eigenproblem routines is to compute values of 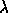 and, optionally, corresponding vectors z for a given matrix A.
and, optionally, corresponding vectors z for a given matrix A.
This computation proceeds in the following stages:
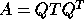 with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is
with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is 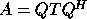 with Q unitary and T, as before,
real symmetric tridiagonal .
with Q unitary and T, as before,
real symmetric tridiagonal .
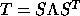 , where S is orthogonal and
, where S is orthogonal and 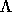 is diagonal.
The diagonal entries of
is diagonal.
The diagonal entries of 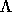 are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z = QS, so that
are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z = QS, so that 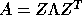 (
(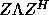 when
A is complex Hermitian).
when
A is complex Hermitian).
In the real case, the decomposition 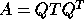 is computed by one
of the routines xSYTRD , xSPTRD, or xSBTRD,
depending on how the matrix is
stored (see Table 2.10). The complex analogues of these routines
are called xHETRD, xHPTRD, and xHBTRD.
The routine xSYTRD (or xHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 5.4.
The routine xORGTR (or in the complex case xUNMTR) is
provided to form Q explicitly;
this is needed in particular
before calling xSTEQR to compute all the eigenvectors of A
by the QR algorithm.
The routine xORMTR (or in the complex case xUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T computed by xSTEIN, back to eigenvectors of A.
is computed by one
of the routines xSYTRD , xSPTRD, or xSBTRD,
depending on how the matrix is
stored (see Table 2.10). The complex analogues of these routines
are called xHETRD, xHPTRD, and xHBTRD.
The routine xSYTRD (or xHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section 5.4.
The routine xORGTR (or in the complex case xUNMTR) is
provided to form Q explicitly;
this is needed in particular
before calling xSTEQR to compute all the eigenvectors of A
by the QR algorithm.
The routine xORMTR (or in the complex case xUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T computed by xSTEIN, back to eigenvectors of A.
When packed storage is used, the corresponding routines for forming Q or multiplying another matrix by Q are xOPGTR and xOPMTR (in the complex case, xUPGTR and xUPMTR).
When A is banded and xSBTRD (or xHBTRD) is used to reduce it to tridiagonal form , Q is determined as a product of Givens rotations , not as a product of elementary reflectors; if Q is required, it must be formed explicitly by the reduction routine. xSBTRD is based on the vectorizable algorithm due to Kaufman [57].
There are several routines for computing eigenvalues and eigenvectors of T, to cover the cases of computing some or all of the eigenvalues, and some or all of the eigenvectors. In addition, some routines run faster in some computing environments or for some matrices than for others. Also, some routines are more accurate than other routines.
 or
or 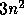 ).
See [67][47][15] for details.
).
See [67][47][15] for details.
See Table 2.10.
------------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
------------------------------------------------------------------------------
dense symmetric tridiagonal reduction SSYTRD CHETRD DSYTRD ZHETRD
(or Hermitian)
------------------------------------------------------------------------------
packed symmetric tridiagonal reduction SSPTRD CHPTRD DSPTRD ZHPTRD
(or Hermitian)
------------------------------------------------------------------------------
band symmetric tridiagonal reduction SSBTRD CHBTRD DSBTRD ZHBTRD
(or Hermitian)
orthogonal/unitary generate matrix after SORGTR CUNGTR DORGTR ZUNGTR
reduction by xSYTRD
multiply matrix after SORMTR CUNMTR DORMTR ZUNMTR
reduction by xSYTRD
------------------------------------------------------------------------------
orthogonal/unitary generate matrix after SOPGTR CUPGTR DOPGTR ZUPGTR
(packed storage) reduction by xSPTRD
multiply matrix after SOPMTR CUPMTR DOPMTR ZUPMTR
reduction by xSPTRD
------------------------------------------------------------------------------
symmetric eigenvalues/ SSTEQR CSTEQR DSTEQR ZSTEQR
tridiagonal eigenvectors via QR
eigenvalues only SSTERF DSTERF
via root-free QR
eigenvalues only SSTEBZ DSTEBZ
via bisection
eigenvectors by SSTEIN CSTEIN DSTEIN ZSTEIN
inverse iteration
------------------------------------------------------------------------------
symmetric eigenvalues/ SPTEQR CPTEQR DPTEQR ZPTEQR
tridiagonal eigenvectors
positive definite
------------------------------------------------------------------------------
Table 2.10: Computational routines for the symmetric eigenproblem