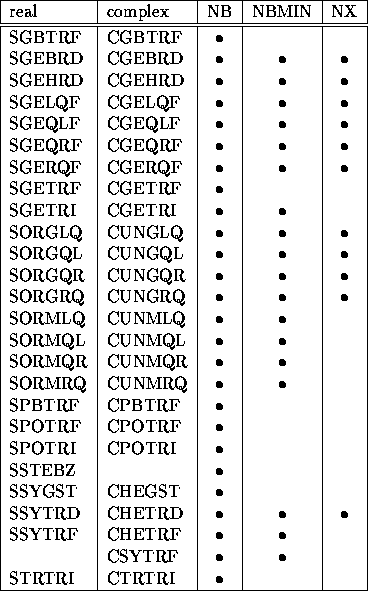
Table 6.1: Use of the block parameters NB, NBMIN, and NX in LAPACK
Machine-dependent parameters such as the block size are set by calls to an inquiry function which may be set with different values on each machine. The declaration of the environment inquiry function is
INTEGER FUNCTION ILAENV( ISPEC, NAME, OPTS, N1, N2, N3, N4 )where ISPEC, N1, N2, N3, and N4 are integer variables and NAME and OPTS are CHARACTER*(*). NAME specifies the subroutine name: OPTS is a character string of options to the subroutine; and N1-N4 are the problem dimensions. ISPEC specifies the parameter to be returned; the following values are currently used in LAPACK:
ISPEC = 1: NB, optimal block size
= 2: NBMIN, minimum block size for the block routine
to be used
= 3: NX, crossover point (in a block routine, for
N < NX, an un blocked routine should be used)
= 4: NS, number of shifts
= 6: NXSVD is the threshold point for which the QR
factorization is performed prior to reduction to
bidiagonal form. If M > NXSVD * N, then a
QR factorization is performed.
= 8: MAXB, crossover point for block multishift QR
The three block size parameters, NB, NBMIN, and NX, are used in many different subroutines (see Table 6.1). NS and MAXB are used in the block multishift QR algorithm, xHSEQR. NXSVD is used in the driver routines xGELSS and xGESVD.

Table 6.1: Use of the block parameters NB, NBMIN, and NX in LAPACK
The LAPACK testing and timing programs use a special version of ILAENV where the parameters are set via a COMMON block interface. This is convenient for experimenting with different values of, say, the block size in order to exercise different parts of the code and to compare the relative performance of different parameter values.
The LAPACK timing programs were designed to collect data for all the routines in Table 6.1. The range of problem sizes needed to determine the optimal block size or crossover point is machine-dependent, but the input files provided with the LAPACK test and timing package can be used as a starting point. For subroutines that require a crossover point, it is best to start by finding the best block size with the crossover point set to 0, and then to locate the point at which the performance of the unblocked algorithm is beaten by the block algorithm. The best crossover point will be somewhat smaller than the point where the curves for the unblocked and blocked methods cross.
For example, for SGEQRF on a single processor of a CRAY-2, NB = 32 was observed to be a good block size , and the performance of the block algorithm with this block size surpasses the unblocked algorithm for square matrices between N = 176 and N = 192. Experiments with crossover points from 64 to 192 found that NX = 128 was a good choice, although the results for NX from 3*NB to 5*NB are broadly similar. This means that matrices with N < = 128 should use the unblocked algorithm, and for N > 128 block updates should be used until the remaining submatrix has order less than 128. The performance of the unblocked (NB = 1) and blocked (NB = 32) algorithms for SGEQRF and for the blocked algorithm with a crossover point of 128 are compared in Figure 6.1.

Figure 6.1: QR factorization on CRAY-2 (1 processor)
By experimenting with small values of the block size, it should be straightforward to choose NBMIN, the smallest block size that gives a performance improvement over the unblocked algorithm. Note that on some machines, the optimal block size may be 1 (the unblocked algorithm gives the best performance); in this case, the choice of NBMIN is arbitrary. The prototype version of ILAENV sets NBMIN to 2, so that blocking is always done, even though this could lead to poor performance from a block routine if insufficient workspace is supplied (see chapter 7).
Complicating the determination of optimal parameters is the fact that
the orthogonal factorization routines and SGEBRD accept non-square
matrices as input.
The LAPACK timing program allows M and N to be varied independently.
We have found the optimal block size to be
generally insensitive to the shape of the matrix,
but the crossover point is more dependent on the matrix shape.
For example, if
M >> N in the QR factorization, block updates
may always be faster than unblocked updates on the remaining submatrix,
so one might set NX = NB if M > = 2N.
Parameter values for the number of shifts, etc. used to tune the block multishift QR algorithm can be varied from the input files to the eigenvalue timing program. In particular, the performance of xHSEQR is particularly sensitive to the correct choice of block parameters. Setting NS = 2 will give essentially the same performance as EISPACK . Interested users should consult [3] for a description of the timing program input files.