Footnotes
- ...
- If we tried
to compute the trivial eigenvalues in the same way as the nontrivial
ones, that is by taking ratios of the leading
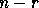 diagonal entries
of
diagonal entries
of 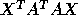 and
and 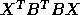 , we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [43].
, we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [43].
- ...
-
If
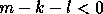 , we may add some zero rows to
, we may add some zero rows to 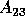 to make
it upper triangular.
to make
it upper triangular.
- ...
- This is the
case on Cybers, Cray X-MP, Cray Y-MP, Cray 2 and Cray C90.
- ...
- See subsection 2.1.3 for explanation
of the naming convention used for LAPACK routines.
- ...
- Important machines that do not implement the IEEE standard
include the Cray XMP, Cray YMP, Cray 2, Cray C90, IBM 370 and DEC Vax.
Some architectures have two (or more) modes, one that implements IEEE
arithmetic, and another that is less accurate but faster.
- ...
- Machines implementing IEEE arithmetic can continue to compute
past overflows, and even division by zero, square roots of negative numbers, etc.,
by producing infinity and NaN (``Not a Number'') symbols. These are
special floating-point numbers subject to special rules of arithmetic.
The default on many systems is to
continue computing with these symbols, rather than giving an error message,
which would often be more convenient for debugging.
It is also possible to stop with an error message. The user should consult
the system manual to see how to turn error messages on or off.
- ...
-
Sometimes our algorithms satisfy only
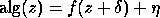 where both
where both
 and
and 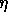 are small. This does not significantly change the following
analysis.
are small. This does not significantly change the following
analysis.
- ...
- More generally,
we only need Lipschitz continuity of
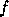 , and may use the Lipschitz
constant in place of
, and may use the Lipschitz
constant in place of 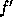 in deriving error bounds.
in deriving error bounds.
- ...
- This is
a different use of the term ill-posed than used in other contexts. For
example, to be well-posed (not ill-posed) in the sense of Hadamard,
it is sufficient for
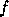 to be continuous,
whereas we require Lipschitz continuity.
to be continuous,
whereas we require Lipschitz continuity.
- ...
- There are some
caveats to this statement. When computing the inverse of a matrix,
the backward error
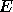 is small taking the
columns of the computed inverse one at
a time, with a different
is small taking the
columns of the computed inverse one at
a time, with a different 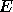 for each column [38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of
for each column [38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of 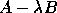 ,
, 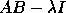 or
or 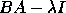 ,
with
,
with 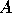 symmetric and
symmetric and 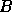 symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
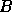 has a large condition number
has a large condition number 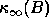 ,
although it has useful error bounds in this case too
(see section 4.10). Solving the Sylvester equation
,
although it has useful error bounds in this case too
(see section 4.10). Solving the Sylvester equation
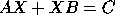 for the matrix
for the matrix 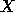 may not be backward stable, although
there are again useful error bounds for
may not be backward stable, although
there are again useful error bounds for 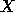 [54].
[54].
- ...
- For other algorithms, the answers (and computed error bounds)
are as accurate as though the algorithms were componentwise relatively backward
stable, even though they are not. These algorithms are called
componentwise relatively forward stable.
- ...
- As discussed in
section 4.2, this approximate error bound
may underestimate the true error by a factor
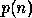 which is a modestly growing function of the problem dimension
which is a modestly growing function of the problem dimension  .
Often
.
Often 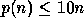 .
.
- ...
- This and other numerical examples
were computed in IEEE single precision arithmetic [4]
on a DEC 5000/120 workstation.
- ...
- These bounds are special
cases of those in section 4.8.
- ...
- Although such a one-to-one
correspondence between computed and true eigenvalues exists, it is not as
simple to describe as in the symmetric case. In the symmetric case the eigenvalues
are real and simply sorting provides the one-to-one correspondence,
so that
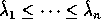 and
and 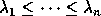 . With nonsymmetric matrices
. With nonsymmetric matrices
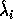 is usually just the computed eigenvalue closest to
is usually just the computed eigenvalue closest to
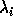 , but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let
, but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let 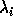 be the eigenvalues
of
be the eigenvalues
of 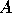 and
and 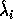 be the eigenvalues of
be the eigenvalues of 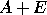 . Let
. Let
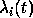 be the eigenvalues of
be the eigenvalues of 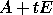 , where
, where 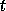 is a parameter,
which is initially zero, so that we may set
is a parameter,
which is initially zero, so that we may set 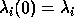 .
As
.
As 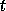 increase from 0 to 1,
increase from 0 to 1, 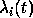 traces out a curve from
traces out a curve from
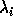 to
to 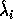 , providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique.
, providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique.
- ...
- These bounds are special
cases of those in sections 4.7 and 4.8,
since the singular values
and vectors of
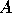 are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix
are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix 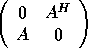 [p. 427]GVL2.
[p. 427]GVL2.
- ...
- This bound is guaranteed
only if the Level 3 BLAS are implemented in a conventional way,
not in a fast way as described in section 4.13.
- ...
- Another interpretation of chordal distance is as half the usual
Euclidean distance between the projections of
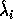 and
and
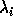 on the Riemann sphere, i.e., half the length of the chord
connecting the projections.
on the Riemann sphere, i.e., half the length of the chord
connecting the projections.
- ...
-
(Input or output) means that the argument may be either an input argument or
an output argument, depending on the values of other arguments;
for example, in the xyySVX driver routines, some arguments are used either
as output arguments to return details of a factorization, or as input
arguments to supply details of a previously computed factorization.
- ...
-
(Workspace/output) means that the argument is used principally as a work
array, but may also return some useful information (in its first
element)
- ...
- Changing
DBLE to DREAL must be selective, because instances of DBLE with an integer
argument must not be changed. The compiler should flag any instances
of DBLE with a COMPLEX*16 argument if it does not accept them.
- ...
- The requirement is stated ``LDA
 max(1,N)''
rather than simply
``LDA
max(1,N)''
rather than simply
``LDA  N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.
N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.
Tue Nov 29 14:03:33 EST 1994
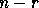 diagonal entries
of
diagonal entries
of 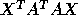 and
and 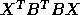 , we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [43].
, we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in [43].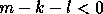 , we may add some zero rows to
, we may add some zero rows to 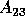 to make
it upper triangular.
to make
it upper triangular.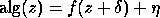 where both
where both
 and
and 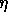 are small. This does not significantly change the following
analysis.
are small. This does not significantly change the following
analysis.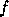 , and may use the Lipschitz
constant in place of
, and may use the Lipschitz
constant in place of 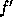 in deriving error bounds.
in deriving error bounds.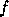 to be continuous,
whereas we require Lipschitz continuity.
to be continuous,
whereas we require Lipschitz continuity.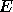 is small taking the
columns of the computed inverse one at
a time, with a different
is small taking the
columns of the computed inverse one at
a time, with a different 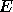 for each column [38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of
for each column [38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of 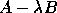 ,
, 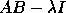 or
or 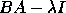 ,
with
,
with 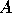 symmetric and
symmetric and 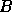 symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
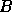 has a large condition number
has a large condition number 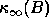 ,
although it has useful error bounds in this case too
(see section 4.10). Solving the Sylvester equation
,
although it has useful error bounds in this case too
(see section 4.10). Solving the Sylvester equation
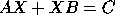 for the matrix
for the matrix 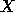 may not be backward stable, although
there are again useful error bounds for
may not be backward stable, although
there are again useful error bounds for 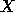 [54].
[54].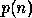 which is a modestly growing function of the problem dimension
which is a modestly growing function of the problem dimension  .
Often
.
Often 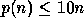 .
.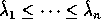 and
and 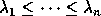 . With nonsymmetric matrices
. With nonsymmetric matrices
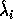 is usually just the computed eigenvalue closest to
is usually just the computed eigenvalue closest to
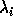 , but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let
, but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let 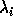 be the eigenvalues
of
be the eigenvalues
of 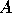 and
and 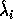 be the eigenvalues of
be the eigenvalues of 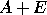 . Let
. Let
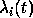 be the eigenvalues of
be the eigenvalues of 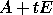 , where
, where 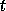 is a parameter,
which is initially zero, so that we may set
is a parameter,
which is initially zero, so that we may set 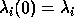 .
As
.
As 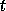 increase from 0 to 1,
increase from 0 to 1, 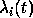 traces out a curve from
traces out a curve from
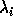 to
to 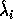 , providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique.
, providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique.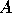 are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix
are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix 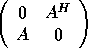 [p. 427]GVL2.
[p. 427]GVL2.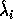 and
and
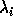 on the Riemann sphere, i.e., half the length of the chord
connecting the projections.
on the Riemann sphere, i.e., half the length of the chord
connecting the projections. max(1,N)''
rather than simply
``LDA
max(1,N)''
rather than simply
``LDA  N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.
N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.